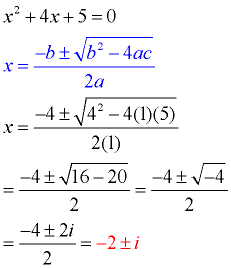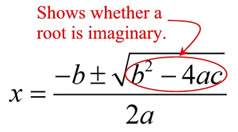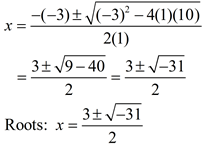Find All Real and Imaginary Solutions to the Equation

See Quadratic Formula for a refresher on using the formula. In Algebra 1, you found that certain quadratic equations had negative square roots in their solutions. Upon investigation, it was discovered that these square roots were called imaginary numbers and the roots were referred to as complex roots. Let's refresh these findings regarding quadratic equations and then look a little deeper. Quadratic Equations and Roots Containing "i ": In relation to quadratic equations, imaginary numbers (and complex roots) occur when the value under the radical portion of the quadratic formula is negative. When this occurs, the equation has no roots (or zeros) in the set of real numbers. The roots belong to the set of complex numbers, and will be called "complex roots" (or "imaginary roots"). These complex roots will be expressed in the form a ± bi. A quadratic equation is of the form ax 2 + bx + c = 0 where a, b and c are real number values with a not equal to zero. Consider this example: Find the roots: x 2 + 4x + 5 = 0 This quadratic equation is not factorable, so we apply the quadratic formula. Notice that after combining the values, we are left with a negative value under the square root radical. This negative square root creates an imaginary number (a number containing "i ") . The graph of this quadratic function shows that there are no real roots (zeros) because the graph does not cross the x-axis. Such a graph tells us that the roots of the equation are complex numbers, and will appear in the form a ± bi. 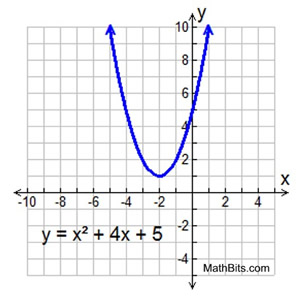The complex roots in this example are x = -2 + i and x = -2 - i. These roots are identical except for the "sign" separating the two terms. One root is -2 PLUS i and the other root is -2 MINUS i. Roots that possess this pattern are called complex conjugates (or conjugate pairs). This pattern of complex conjugates will occur in every set of complex roots that you will encounter when solving a quadratic equation. When expressed as factors and multiplied, these complex conjugates will allow for the middle terms containing "i "s to cancel out. (x - (-2 + i)) • (x - (-2- i)) = (x + 2 - i)•(x + 2 + i) = x 2 + 2x + xi + 2x + 4 + 2i - xi - 2i - i 2 (notice the terms that will cancel) = x 2 + 4x + 4 - (-1) = x 2 + 4x + 5 If the middle terms did not cancel, there would be "i "s in the coefficients, which is not allowed in a quadratic equation. If the roots of a quadratic equation are imaginary, they always occur in conjugate pairs. The Quadratic Formula Indicates Roots Containing "i ": Imaginary or complex roots will occur when the value under the radical portion of the quadratic formula is negative. Notice that the value under the radical portion is represented by "b 2 - 4ac" . So, if b 2 - 4ac is a negative value, the quadratic equation is going to have complex conjugate roots (containing "i "s). b 2 - 4ac is called the discriminant. 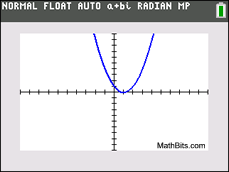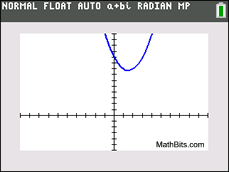If the discriminant is negative, you have a negative under the radical and the roots of the quadratic equation will be complex conjugates. The discriminant, b 2 - 4ac , offers valuable information about the "nature" of the roots of a quadratic equation where a, b and c are rational values. It quickly tells you if the equation has two real roots (b 2 - 4ac > 0), one real repeated root (b 2 - 4ac = 0) or two complex conjugate roots (b 2 - 4ac < 0). If you are trying to determine the "type" of roots of a quadratic equation (not the actual roots themselves), you need not complete the entire quadratic formula. Simply look at the discriminant. DISCRIMINANT: "What type of roots do we have?" POSITIVE b 2 - 4ac > 0 ZERO b 2 - 4ac = 0 NEGATIVE b 2 - 4ac < 0 x 2 + 6x + 5 = 0 discriminant: b 2 - 4ac = 62 - 4(1)(5) = 16 (positive) There are two real roots. There are two x-intercepts. (If the discriminant is a perfect square, the two roots are rational numbers. If the discriminant is not a perfect square, the two roots are irrational numbers containing a radical ( not an "i ".) x 2 + 6x + 5 = (x + 1)(x + 5) = 0 Roots: x = -1, x = -5 x 2 - 2x+ 1 = 0 discriminant: b 2 - 4ac = (-2)2-4(1)(1) = 0 (zero) There is one real root. There is one x-intercept. (The root is repeated.) x 2 - 2x+ 1 = (x - 1)2 = (x - 1)(x - 1) = 0 Repeated root: x = 1 x 2 - 3x + 10 = 0 discriminant: b 2 - 4ac = (-3)2-4(1)(10) = -31 (negative) There are two complex roots. There are no x-intercepts. When graphing, if the vertex of the quadratic function lies above the x-axis, and the parabola opens upward, there will be NO x-intercepts and no real roots to the equation. The equation will have complex conjugate roots. The same applies if the vertex lies below the x-axis, and opens down. NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".

Find All Real and Imaginary Solutions to the Equation

Source: https://mathbitsnotebook.com/Algebra2/Quadratics/QDQuadratics.html

Share :